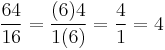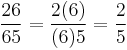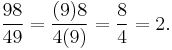Anomalous cancellation
An anomalous cancellation or accidental cancellation is a particular kind of arithmetic procedural error that gives a numerically correct answer. An attempt is made to reduce a fraction by canceling individual digits in the numerator and denominator. This is not a legitimate operation, and does not in general give a correct answer, but in some rare cases the result is numerically the same as if a correct procedure had been applied.[1]
Examples of anomalous cancellations which still produce the correct result include:
The article by Boas analyzes two-digit cases in bases other than base 10, e.g., 32/13 = 2/1 is the only solution in base 4.[2]
References
- ^ Weisstein, Eric W., "Anomalous Cancellation" from MathWorld.
- ^ a b Boas, R. P. "Anomalous Cancellation." Ch. 6 in Mathematical Plums (Ed. R. Honsberger). Washington, DC: Math. Assoc. Amer., pp. 113–129, 1979.